| |||
| |||
| |||
| |||
| |||
| |||
Today, the Internet provides the most efficient and commonly used information highway for communication and information exchange. With millions of people communicating on this highway, privacy has become an extremely important issue.
Secure communication is becoming pivotal in every network design. For this reason, cryptography is one of the essential elements of today's information systems, providing secure access to information with greater reliability, authenticity, accuracy, and confidentiality.
This chapter provides an overview of cryptography solutions and various types of virtual private network (VPN) deployments. This chapter builds foundation knowledge of cryptographic algorithms and protocols for the next chapter by covering IPsec VPN that employs a cryptography approach.
From the physical layer to the application layer of the OSI reference model, cryptography is the first of many steps necessary to provide secure communication solutions.
A cryptosystem—or "cryptographic system"—is a framework that involves the application of cryptography to provide secure communications.
A cryptosystem is the collection of protocols, procedures, and algorithms required to implement an encoding and decoding system using cryptography technology.
With a cryptosystem, the confidentiality and integrity of information can be achieved by using various methods that employ cryptography, such as encryption and decryption techniques, hash functions, digital signatures, key management techniques, and various other systems.
Cryptography is an ancient science. As far back as 1900 B.C., Egyptians used cryptography for ancient inscriptions. Romans used some early cryptosystems to exchange confidential messages.
The word cryptography comes from the Greek words kryptos and graphein. Kryptos means "hidden" and graphein means "writing." Hence, cryptography is said to be the study of hidden writing, or the science of encrypting and decrypting normal text to make it incomprehensible.
Cryptographic techniques are usually classified as
Traditional: Traditional techniques date back centuries and use simple mechanisms of transposition (reordering of plaintext mechanisms) and substitution (alteration of plaintext mechanisms).
Modern: Modern techniques rely on sophisticated protocols and algorithms to achieve assurance of information security.
In data and telecommunications, cryptography is necessary when communicating over untrusted or shared mediums, such as the Internet.
Cryptographic technologies and solutions help address issues related to information confidentiality, integrity, and access control. The objective is to protect the immobile and mobile (stationary or during transmission) information by using cryptographic technologies. Cryptography solutions also provide techniques for identifying unauthorized data modifications and alterations.
In the modern world of computer networks, information and information systems are digitally secured by using modern cryptographic protocols and algorithms.
The following terminologies are commonly used in cryptographic context to describe a function or a role. Here are some basic terms used throughout the chapter and further:
Encryption: The use of an algorithmic process that uses a secret key to transform plain data into a secret code, to prevent anyone except the intended recipient from accessing the information. Encryption is the process of obscuring information to make it unreadable to unauthorized recipients. Encryption provides a means of secure communication over an insecure communications medium. Figure 14-1 illustrates how the encryption process works.
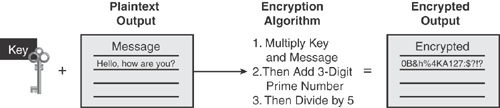
Decryption: The reverse process of encryption, converting encrypted data back into its original form.
Plaintext: The original unencrypted data.
Ciphertext: The product of the encryption process—the data that has been encrypted.
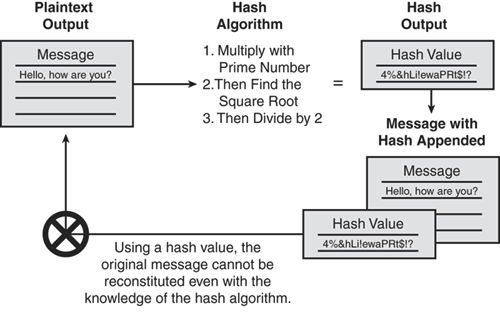
Hash: A hash value, also known as a message digest value that is a mathematically generated unique number from a sequence of text by applying a mathematical formula. Hash is a value calculated from the original data to uniquely identify the data. Figure 14-2 illustrates how the hash function produces a unique hash value by using a mathematical algorithm, which is then appended to the original message as the unique identifier (like a fingerprint of the message).
Note
While explaining cryptography in various paragraphs and diagrams in this chapter, two communicating endpoints are referred to as "Alice" and "Bob" to identify the communicating parties. This is a common nomenclature in cryptographic literatures.
In general, there are three types of cryptographic algorithms:
Symmetric key cryptography (also known as secret key or preshared key cryptography): Uses a single key for both the encryption and decryption process.
Asymmetric key Cryptography (also known as public Key cryptography): Uses a two-key pair, one key for the encryption and another for the decryption process.
Hash algorithm (or hash function): Uses a one-way mathematical function to produce an algorithmically randomized unique hash value to identify the data that is unique from other data. Using a hash value, the original message cannot be reconstituted even with the knowledge of the hash algorithm.
All three types of cryptography schemes have unique function mapping to specific applications. For example, the symmetric key cryptography approach is typically used for the encryption of data providing confidentiality, whereas asymmetric key cryptography is mainly used in key exchange and nonrepudiation, thereby providing confidentiality and authentication. The hash algorithm (noncryptic), on the other hand, does not provide confidentiality but provides message integrity, and cryptographic hash algorithms provide message integrity and identity of peers during transport over insecure channels.
A symmetric key cryptography, also known as a secret-key or preshared key algorithm, is an approach that uses a single key for both encryption and decryption. Symmetric key cryptography is typically used to encrypt the contents of a message to provide data confidentiality.
Figure 14-3 depicts how the symmetric key encryption process works in using the same single key on both ends. The key must be known to both ends. The sender (Bob) uses a secret key to encrypt the plaintext message and thereby produce the ciphertext, and the receiver (Alice) uses the same secret key to decrypt the ciphertext, thereby producing the original plaintext message. A single key is used for both functions; hence, this method is called the symmetric encryption process.
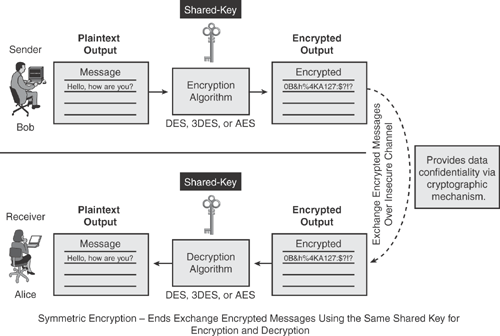
Symmetric key cryptography ciphers are generally categorized in two modes:
Stream cipher: A symmetric cipher that encrypts the plaintext digits (bits or bytes) one by one. The transformation of encrypted output varies during the encryption cycle. There are several varying types of stream ciphers, such as synchronous stream cipher and asynchronous stream cipher. RC4 is one of the most common stream cipher designs.
Block cipher: A symmetric key cipher that encrypts the plaintext on a fixed-length group of bits, with an unvarying transformation during the encryption cycle. Block ciphers encrypt blocks of data by using the same key on each block. For example, a block cipher can take a 128-bit block of plaintext as input and generate a corresponding 128-bit block of ciphertext output. DES and AES are examples of common block cipher designs.
In general, a block cipher mode yields the same ciphertext from a block of plaintext when using the same key, whereas a stream cipher mode yields different ciphertext from the same plaintext. Symmetric key cryptography algorithms are generally much less computationally intensive than asymmetric key cryptography algorithms.
Symmetric key cryptography is less computationally intensive and therefore much faster, especially for bulk data encryption such as data transfers, and can run on appliances without dedicated cryptographic hardware.
The list that follows contains some of the common symmetric key cryptography algorithms that are in use today:
Data Encryption Standard (DES): DES, one of the earliest and most common symmetric key algorithms, was designed by IBM in the 1970s. DES was selected the official Federal Information Processing Standard (FIPS) for the United States in 1976 and was adopted by the National Institute for Standards and Technology (NIST) in 1977 for commercial and unclassified government applications.
DES is a block cipher that uses a 56-bit key to encrypt 64-bit datagram blocks.
DES is no longer considered very secure, mainly because the inherent 56-bit key size is too small. DES has been known to be compromised in less than 24 hours.
Triple-DES (3DES): 3DES is a variant of DES. 3DES employs up to three 56-bit keys (168-bits) and makes three encryption and decryption passes over the same datagram block. As mentioned earlier, DES is considered insecure because of its small key length. 3DES was derived mainly to enlarge the key length to 168-bits (three times 56-bit DES key) without having to switch to a newer algorithm.
3DES is also a block cipher that uses a 168-bit key to encrypt 64-bit datagram blocks. 3DES is mainly a recommended replacement to all DES implementations.
Advanced Encryption Standard (AES): Advanced Encryption Standard (AES), also known as Rijndael, was introduced by NIST in 2001 and was announced as the new federal cryptographic standard replacing DES. AES became effectively a cryptographic standard in 2002. Today, AES is one of the most commonly used algorithms among the symmetric key cryptography implementations.
The AES algorithm can use a variable block length and key length. Specifications indicate that any combination of key lengths of 128, 192, or 256 bits and block lengths of 128, 192, or 256 bits can be used.
AES is a block-cipher algorithm that is capturing its share and is slowly replacing the predecessor DES and 3DES standards.
Note
Among the common symmetric key cryptography algorithms previously listed, several other symmetric key algorithms are available—namely, CAST-128/256, IDEA, RC4, and Blowfish.
Asymmetric key cryptography is also commonly known as a public-key algorithm and was first described publicly in 1976.
Asymmetric key cryptography design uses a two-key pair: one key is used to encrypt the plaintext, and the other key is used to decrypt the ciphertext. Unlike the symmetric-key approach, two parties can communicate securely over an insecure channel without having to share a secret key. Asymmetric key cryptography is typically used in digital certification and key management. Theoretically, asymmetric key cryptography could also be used to encrypt data, although this is rarely done because symmetric key cryptography is much more efficient and much less computationally intensive than asymmetric key cryptography.
Figure 14-4 depicts how the asymmetric key encryption process works using the two keys known as public and private keys. Each end user has its own pair of public and private keys. The public key from each end user is widely distributed via the key-management system to all users. The private key is never exchanged or revealed to another party.
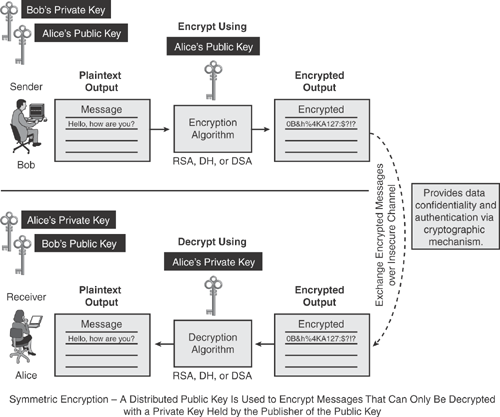
Figure 14-4 shows that the sender (Bob) uses the receiver's (Alice) public key to encrypt the message to produce the ciphertext. When the receiver (Alice) gets the encrypted message, she uses her own private key to decrypt the ciphertext to produce the original plaintext message. This mechanism provides a secure communication exchange, assuring that only the authorized recipient (Alice, in this case) will be able to decipher the message with her own private key.
Another variation of the asymmetric key approach is used to validate the identity of the sender, whereby the sender (Bob) uses his own private key to encrypt the message, and the receiver (Alice) uses the sender's (Bob) public key to decrypt the ciphertext. This variation offers nonrepudiation, in which only the holder of the private key could have encrypted the message, thereby assuring that the sender was the one who sent the message.
Separate keys are used for both functions; therefore, this method is called the asymmetric encryption process.
The list that follows contains some of the common asymmetric key cryptography algorithms that are widely used for key exchange and digital signatures:
RSA: The RSA algorithm was described publicly in 1976 by the three MIT mathematicians who developed this algorithm—Ronald Rivest, Adi Shamir, and Leonard Adleman. RSA is named after the initials from the surnames of the developers.
The RSA algorithm was the first greatest advancement that used the asymmetric key cryptography mechanism. RSA is one of the most popular and widely implemented asymmetric key algorithms that can be used for key exchange, digital signatures, and message encryption.
RSA algorithms are available in varying standards (RC1, RC2, RC3, RC4, RC5, and RC6), all of which use variable size block lengths and key lengths.
Diffie-Hellman (DH): DH was first described publicly in 1976 by Stanford University Professor Martin Hellman and graduate student Whitfield Diffie. The DH algorithm was introduced shortly after the RSA algorithm was published in 1976.
DH is a public-key distributing system (also known as key-exchange protocol) that employs an asymmetric key cryptography mechanism. DH allows two end users that have no prior knowledge of each other to establish a shared secret key over an insecure communications channel. The resulting secret key can be used to encrypt subsequent messages using a symmetric key algorithm.
Contrary to the RSA algorithm, the DH algorithm is not used for authentication or digital signatures. DH is used only for secret-key key exchange.
Digital Signature Algorithm (DSA): DSA is another asymmetric key algorithm proposed by the National Institute for Standards and Technology (NIST) in 1991 for their use in Digital Signature Standard (DSS). DSA is also a Federal Information Processing Standards (FIPS) standard for digital signatures.
DSA is used mainly for digital signature capability to ensure the authentication of messages.
Public-Key Cryptography Standards (PKCS): PKCS is a set of interoperable public-key cryptography standards and guidelines, designed and published by RSA Data Security Inc.
PKCS #1: RSA Cryptography Standard (see RFC 3447).
PKCS #2: Was withdrawn and merged into PKCS #1. It covered RSA encryption of message digests.
PKCS #3: Diffie-Hellman Key-Agreement Standard.
PKCS #4: Was withdrawn and merged into PKCS #1. It covered RSA key syntax.
PKCS #5: Password-Based Encryption Standard (see RFC 2898).
PKCS #6: Extended-Certificate Syntax Standard. It defines extensions to the old X.509v1 certificate specification, obsolete by X.509v3.
PKCS #7: Cryptographic Message Syntax Standard (see RFC 2315). It is used to sign or encrypt messages under a PKI.
PKCS #8: Private-Key Information Syntax Standard.
PKCS #9: Selected Attribute Types (see RFC 2985).
PKCS #10: Certification Request Syntax Standard (see RFC 2986). It defines the format of messages sent to a Certification Authority to request certification of a public key.
PKCS #11: Cryptographic Token Interface Standard (cryptoki). An API defining a generic interface to cryptographic tokens.
PKCS #12: Personal Information Exchange Syntax Standard. It defines a file format commonly used to store private keys with accompanying public-key certificates protected with a password-based symmetric key.
PKCS #13: Elliptic Curve Cryptography (ECC) Standard.
PKCS #14: Pseudo-Random Number Generation (PRNG) Standard. PRNG is an algorithm that generates a sequence of numbers that are not truly random.
PKCS #15: Cryptographic Token Information Format Standard. It defines a standard allowing users of cryptographic tokens to identify themselves to applications, independent of the application's cryptoki implementation (PKCS #11) or other API.
Note
Among the common asymmetric key cryptography algorithms listed previously, several other asymmetric key algorithms are available—namely, Elliptic Curve Cryptography (ECC), Encrypted Key Exchange (EKE), ElGamal, and Cramer-Shoup.
A hash algorithm has a number of names—hash function, message digest, and one-way encryption. Hash algorithms use a mathematical formula to compute a fixed-length hash value based on the original plaintext. Using a hash value, the original message cannot be reconstituted even with the knowledge of the hash algorithm. Hash functions are generally faster than encryption mechanisms.
Hash algorithms are typically used to provide a digital fingerprint of any type of data, to ensure that information has not been altered during the transmission, thus providing a measure for information integrity.
A hash value, also known as a message-digest value, is a unique number that is created from a sequence of text by applying a mathematical formula.
Figure 14-5 illustrates how the hash algorithm works. The sender (Bob) produces a unique hash value by using a mathematical algorithm, which is then appended to the original message as the unique identifier (fingerprint of the message) and transmitted to Alice. The receiver (Alice) separates the appended hash value from the original message and computes the hash locally by using the predetermined hash algorithm. If the locally computed hash equals the appended hash that was received, the data is known to be unaltered, thus providing message integrity.
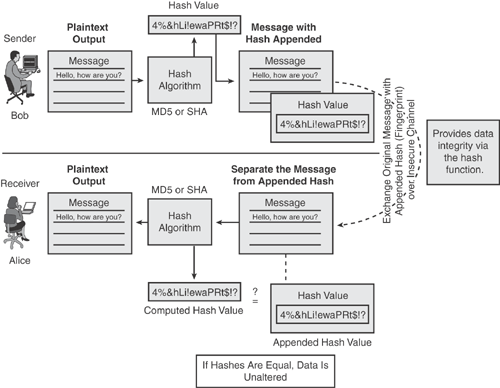
Hash algorithms are commonly used for data integrity check and digital certificates.
The list that follows contains some of the common hash algorithms that are widely used for information integrity, authentication, and digital signatures:
Message Digest (MD) algorithms: Message Digest algorithms are a series of byte-oriented cryptographic hash functions that produce a mathematically computed 128-bit fixed-length hash value (also called message digest or fingerprint) from an arbitrary-length input.
MD2 (see RFC 1319): Developed by Ronald Rivest in 1989. MD2 was designed and optimized for 8-bit machines or systems with limited memory, such as smart cards. First, the message is padded to ensure that its length in bytes is divisible by 16. Then, a 16-byte checksum is appended to the message, and the resulting message is processed to compute a hash value.
MD4 (see RFC 1320): Developed by Ronald Rivest in 1989. MD2 was designed and optimized for 32-bit machines. MD4 was similar to MD2 but designed specifically for faster processing in software. First, the message is padded to ensure that its length in bits plus 64 is divisible by 512. Then a 64-bit binary representation of the original length of the message is concatenated to the message.
MD5 (see RFC 1321): Developed by Ronald Rivest in 1991. MD5 was designed to replace MD4 after potential weaknesses were reported in MD4. MD5 is similar to MD, 4 with enhancements to provide greater security. The MD5 algorithm consists of four distinct rounds, with a slightly different design from that of MD4. Message-digest size and padding requirements remain the same. In spite of several weaknesses reported by numerous cryptographers, MD5 continues to remain popular and is widely used by various products and applications. Algorithmically, MD5 is no longer considered very secure because analytical attacks and practical collisions have been constructed in less than one hour.
Secure Hash Algorithm (SHA): SHA is another series of popular cryptographic hash algorithms that produces 160-bit output. SHA was designed by the National Security Agency (NSA) and published as a U.S. government standard. The SHA algorithm is also used in NIST's Secure Hash Standard (SHS). SHA is computationally slower than MD5 but more secure. The original specification of the SHA algorithm (the first member of the family was known as SHA-0) was introduced in 1993, and two years later, its successor, SHA-1, was published.
SHA-1 (see RFC 3174): The most commonly used hash algorithm in the SHA family, which produces a 160-bit hash value. SHA-1 was considered to be the successor to MD5 and is widely used in a variety of applications and protocols, including Transport Layer Security (TLS), Secure Sockets Layer (SSL), Pretty Good Privacy (PGP), Secure Shell (SSH), Secure Multipurpose Internet Mail Extension (S/MIME), and IPsec. Four additional variants of SHA have since been introduced—namely, SHA-224, SHA-256, SHA-384, and SHA-512 (sometimes collectively referred to as SHA-2). These variants can produce hash values that are 224, 256, 384, or 512 bits in length, respectively. These variants are described in RFC 4634. Cryptographers have reported attacks for both SHA-0 and SHA-1. However, to date, no attacks have yet been reported on the SHA-2 variants.
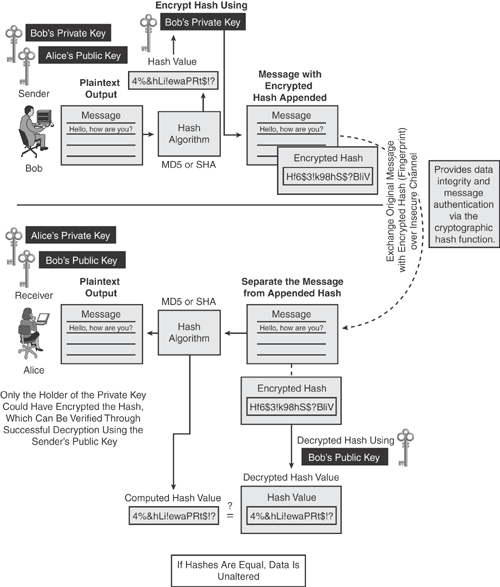
A traditional hash algorithm does not make use of any key mechanism to produce a hash value. However, a cryptographic hash algorithm combined with a secret key is used to calculate a keyed-hash message authentication code (HMAC). Message authentication code (MAC) provides data integrity and message authentication.
Digital signatures use the hash algorithm coupled with the asymmetric key mechanism to produce a private key encrypted hash output. Digital signatures guarantee the authenticity of the message in addition to message integrity.
Figure 14-6 illustrates how the cryptographic keyed-hash algorithm works. The sender (Bob) produces a unique hash value by using a mathematical algorithm, which is then encrypted using Bob's own private key. The encrypted hash value is appended to the original message as the unique identifier (as a fingerprint of the message) and transmitted to Alice. The receiver (Alice) separates the appended encrypted hash value from the original message and decrypts the hash with the sender's (Bob's) public key. Then the receiver takes the original message input through the predetermined hash algorithm to produce a locally generated hash value of the same text. If the locally computed hash equals the unencrypted hash received, the data is known to be unaltered, thus providing message integrity. This process provides nonrepudiation and proof of the integrity and origin of data because it proves that only the holder of the private key could have encrypted the hash, and the private key did so before sending the data. The digital signature provides data integrity and message authentication.
Note
Among the common hash algorithms previously listed, several other hash functions are available—RIPEMD, HAS-160, HAVAL, Whirlpool, and Tiger2.
Tip
Refer to RFC 4270 (by Paul Hoffman and Bruce Schneier, November 2005) for further information on attacks on hash functions, how hash algorithms are susceptible to collision attacks, and how to thwart these known attacks.